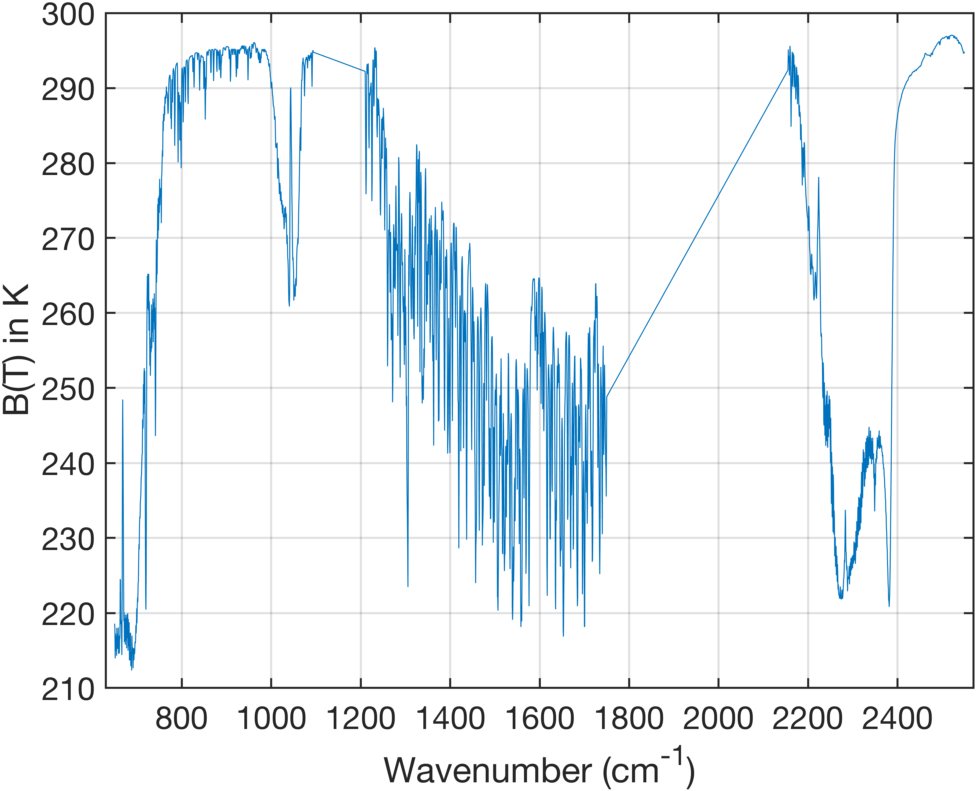
Figure 1 shows the mean BT spectrum for the data under consideration here. Surface temperatures are slightly below 300K on average. For the discussions below pay particular note of the relatively cold radiances near 2380 cm^-1. We cannot directly determine FOV radiance differences from the mean of the clear spectra for the 18 day because: (a) there is no guarantee they are observing identical scenes, and (b) the CrIS FOVs have slightly different mean secant angles which will introduce differences as large as 0.5K in the FOV radiances. Instead of intercompare the FOV biases = (observed - computed) brightness temperature (BT) differences. The computed BTs use the proper secant angle for each scene, so the variation in these biases should only be due to calibration differences among FOVs. Figure 2 shows the ECMWF biases for each of the nine FOVs for this data set.

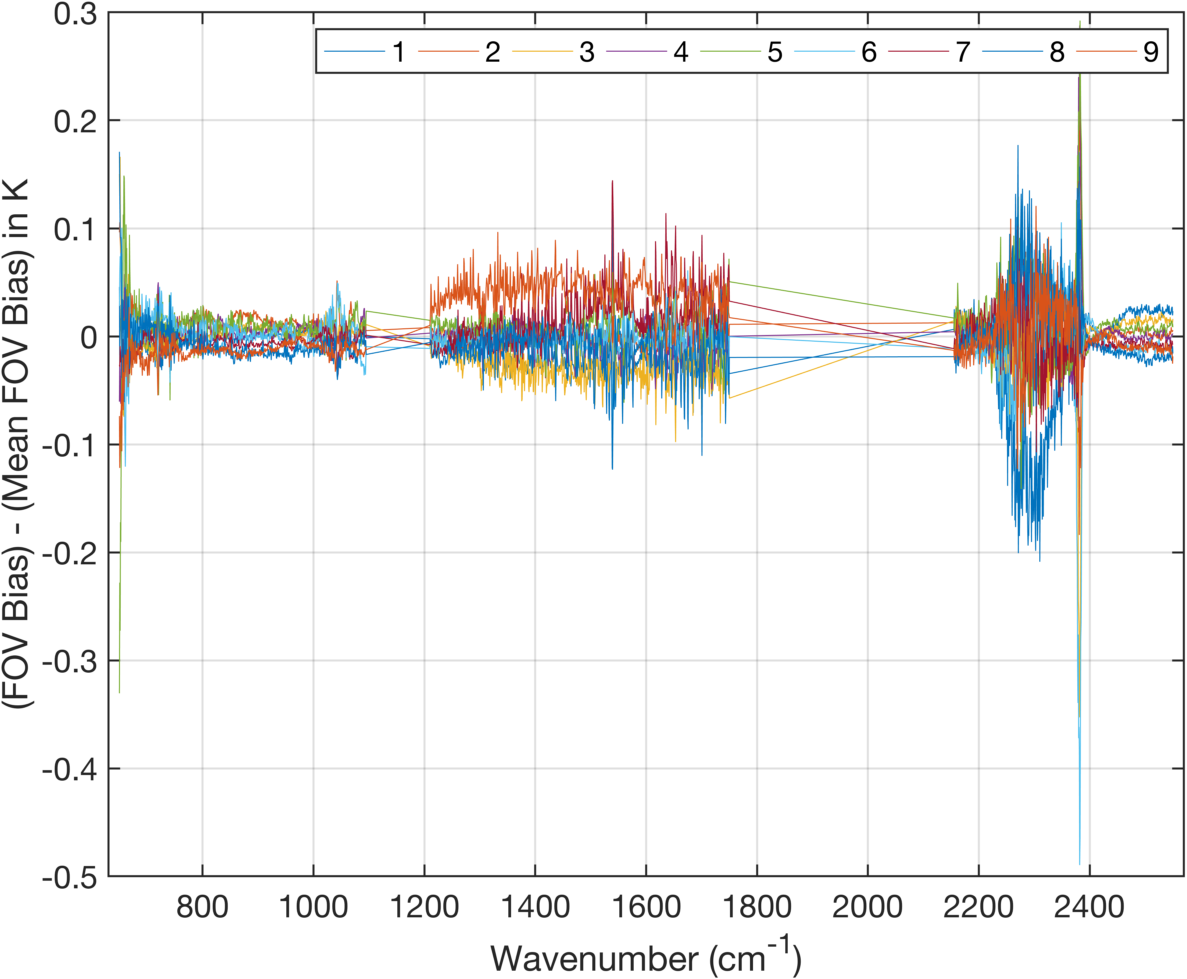
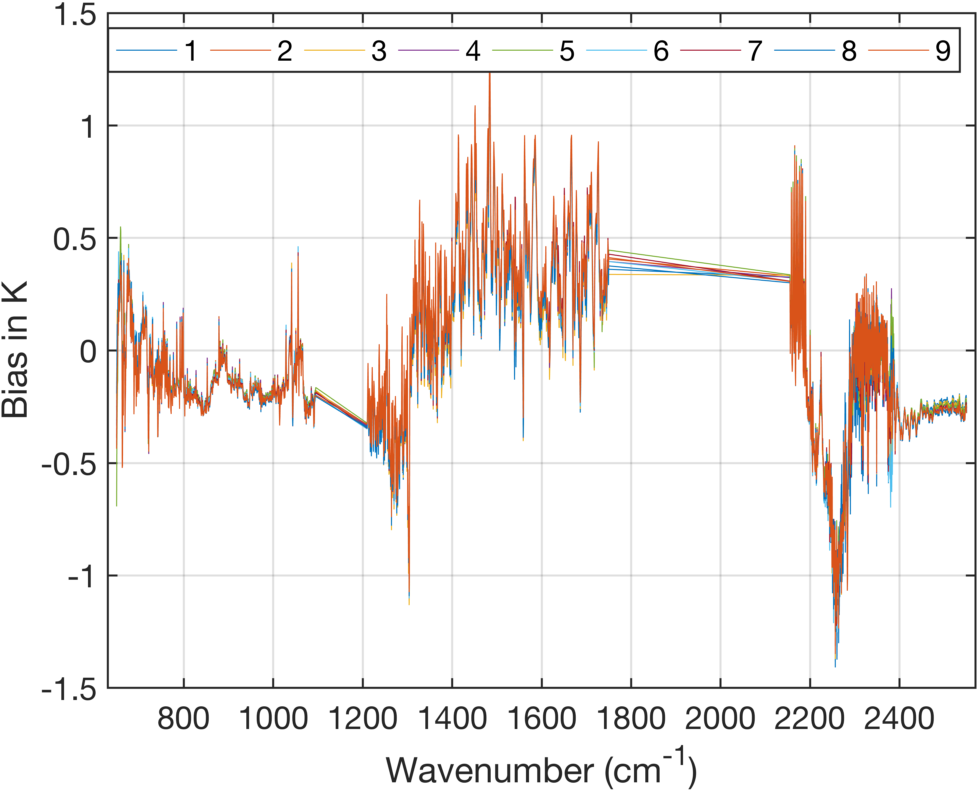
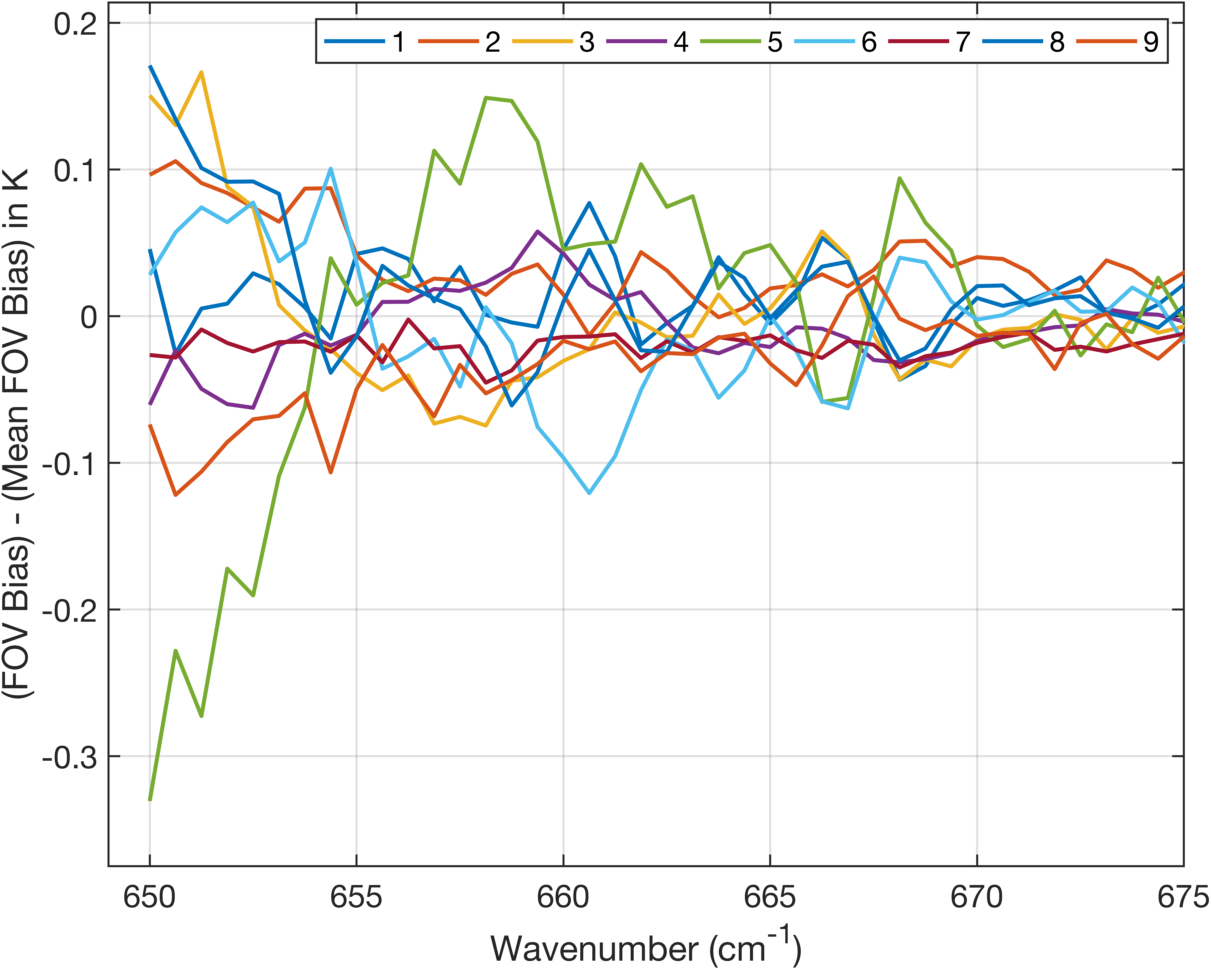
Figure 3 shows the relative differences in the CrIS biases versus ECMWF. Here we are plotting FOV \(bias_i - (\sum_i bias_i)/9\) for \(i=1:9\) By subtracting the mean bias over all FOVs we are left with what are presumably calibration errors. The most visible differences are FOV9 in the midwave, which we have already examined in a previous report. The other two main differences among FOVs is in the extreme longwave and in the 2250-2385 cm^-1 region. The spike near 2380 cm^-1 is in the region of the lowest radiance measured in this band, which leads to high variability in the bias differences (and their standard deviations) when displayed in BT units. A plot of the bias standard deviation in radiance units shows no evidence of a spike, it is almost solely a consequence of the high sensitivity in B(T) to errors in radiance for these channels.

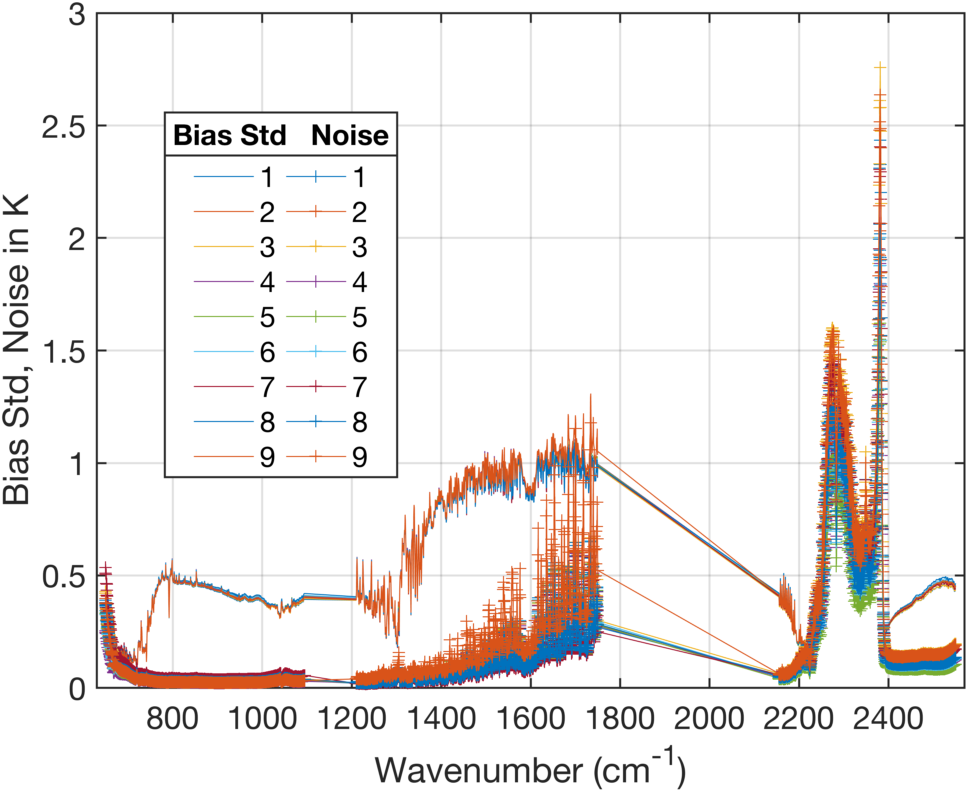
The standard deviations for each FOV bias is shown in Fig. 4, where we have also plotted the measured noise of each FOV. The noise shown is for hamming apodization and includes the effects of the self-apodization corrections on the noise. FOV9 noise is colored differently, just to highlight how different it is in the midwave.

Figure 5 is a zoom of Fig. 3 in the extreme longwave where one can easily see the rather large bias differences among FOVs, especially for FOVs 5 and 6. Similarly in Fig. 6 we show the bias standard deviations, and the CrIS noise, in the same spectral region. These curves vary considerably, presumably because the CrIS noise can vary significantly among FOVs.

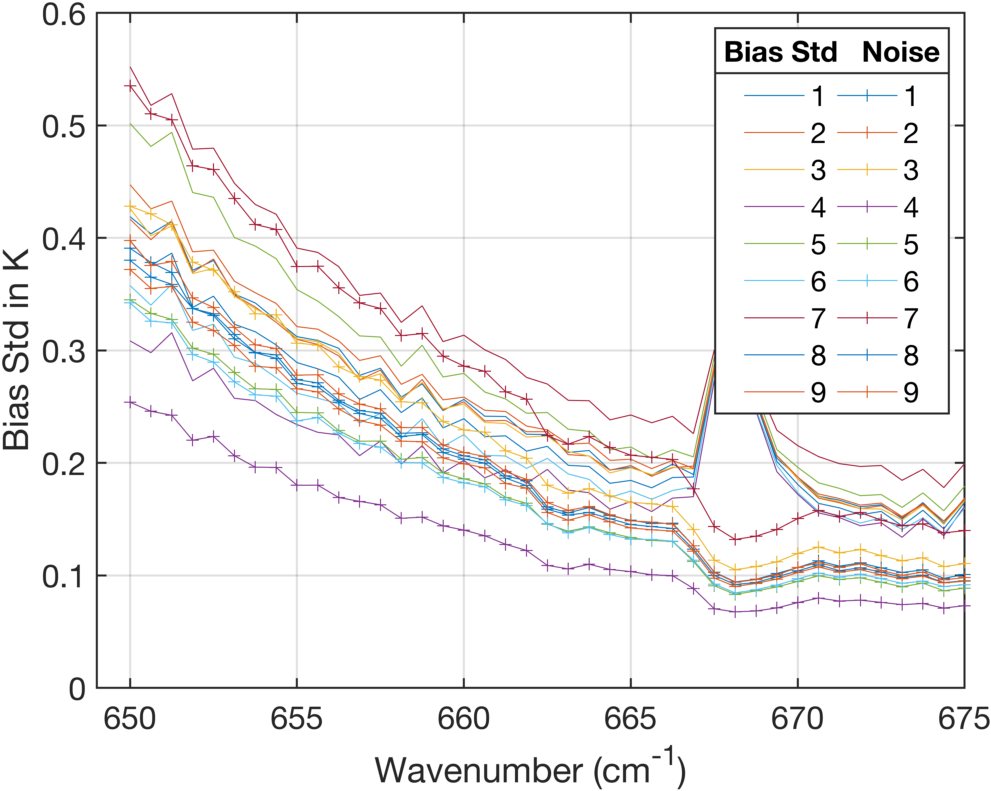
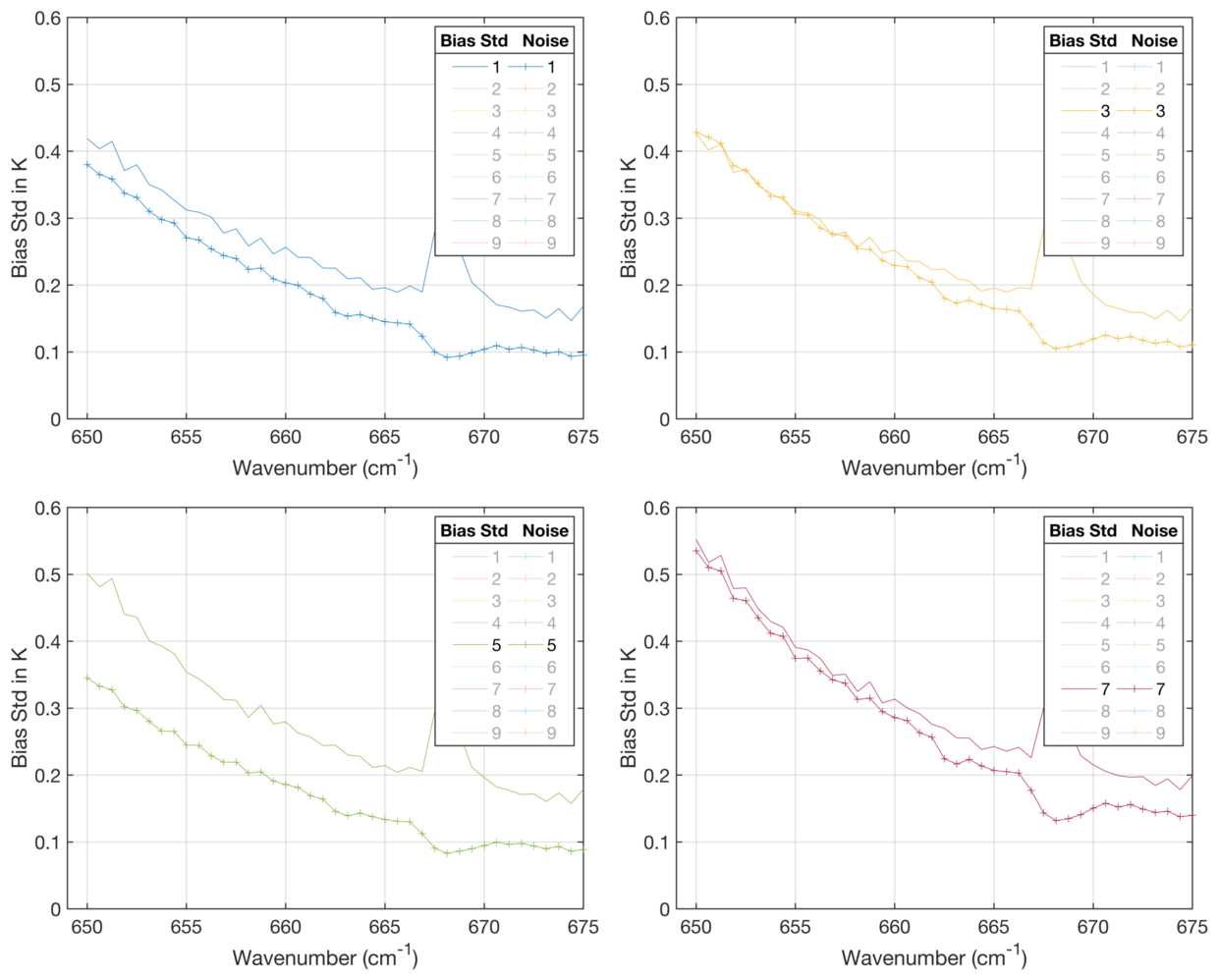
Figure 7 splits out four of the FOVs in Fig. 6 so we can see the relationship between bias standard deviation and noise for a set of representative FOVs. FOV1 in Fig. 7 is closest to the mean, where we see that the bias standard deviation is about 20% higher than the noise. Presumably, this represents the addition of ECMWF model noise (or sampling noise) to the bias standard deviation. Clearly, CrIS noise dominates the bias standard deviation for almost all FOVs. FOV3 in Fig. 7 is a special case, in that the bias standard deviation is dominated by instrument noise, note that only FOV7 has higher noise than FOV3. However, for unknown reasons the FOV3 bias standard deviation contains almost no "model noise". This also means any attempt to derive "model noise" from FOV3 will be highly inaccurate since the bias standard deviation is totally dominated by instrument noise, which seems a bit unphysical. FOV5 in Fig. 7 shows that the FOV5 bias standard deviation is significantly larger than the instrument noise. The FOV7 bias standard deviation and noise shown here are slightly different, but the FOV7 noise is lower than the standard deviation of the bias for all channels.

We use the differences between the FOV noise and the observed ECMWF bias standard deviation to derive what we call "model noise", which is the noise present in the measurement over and above instrument noise. We assume that the model noise is gaussian, and thus is given by

\begin{equation} nedn_{\text{model}} = \sqrt{( bias\_std^2 - nedn_{\text{cris}}^2)} \end{equation}

We then convert \(nedn_{\text{model}}\) to units of brightness temperature and plot the results "model nedt" (or "model noise") in Fig. 8. The darkness of the gray lines is proportional the difference between the radiance bias standard deviation and the instrument noise for each FOV, averaged between 650 to 665 cm^-1. Therefore, for FOVs where the standard deviation and noise are very close, such as FOV3, the color of the "model noise" is very light, since it is highly sensitive to errors.

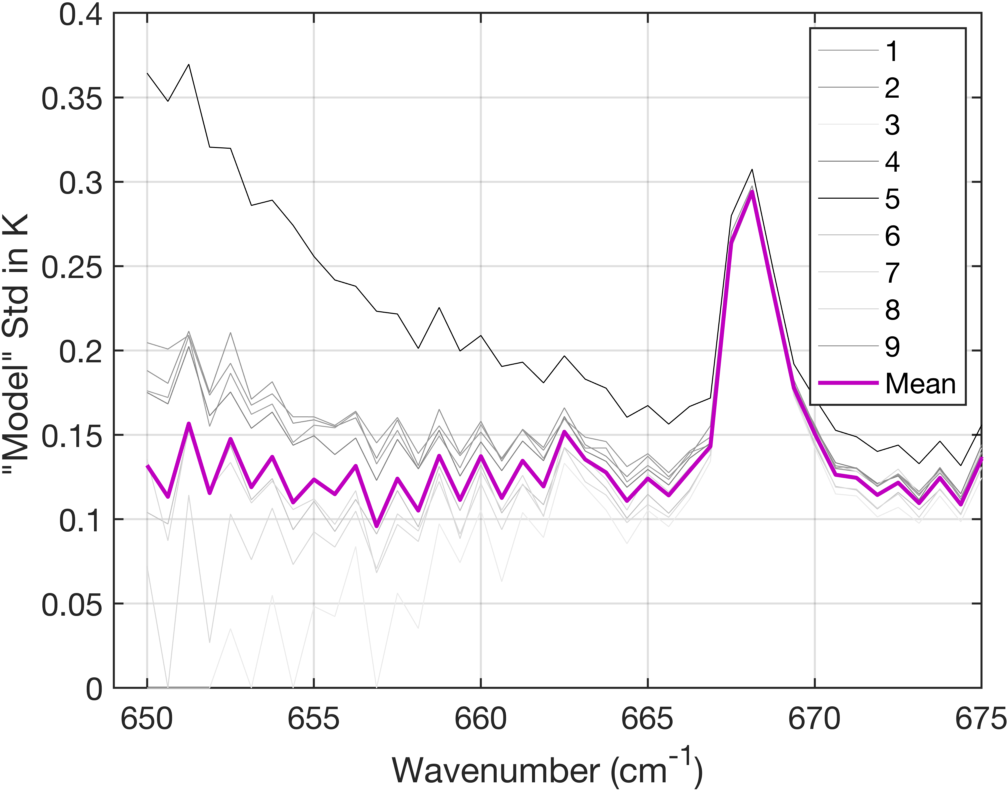
Figure 8 shows quite clearly that FOV5 has a very significant excess of what we are calling "model noise". However, since we are using the same model for each FOV, that excess noise is likely due to noise in the radiance signal. This means that the FOV5 detector has different "noise" in the earth scene than in the ICT scene. In general the mean "model noise" is fairly constant with wavenumber, except for the strong 667 cm^-1 Q-branch which peaks at far higher altitudes than the rest of these channels, and therefore might have different "model noise". In Fig. 9 we re-plot the data in Fig. 8 but this time remove the mean over FOV of the Model Std. and extend the wavenumber scale to 725 cm^-1. This provides a convincing visual that shows the FOV5 excess noise continues to extend well into higher wavenumbers.

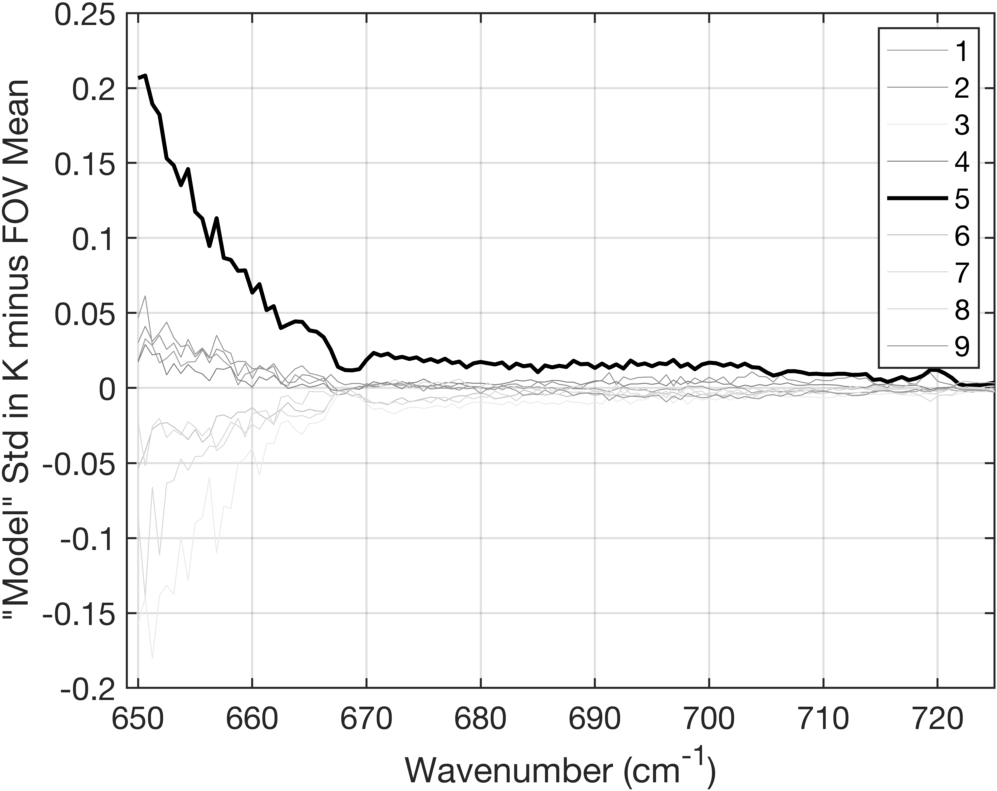
We had some concern that these FOV5 effects might somehow be an artifact of our clear-scene detection algorithm. To address this we produced ECMWF bias for a full day's worth of data for all scenes, using a clear-scene RTA. We then subsetted for clear by requiring that the 902 cm^-1 window channel bias be between -0.5 and +0.5K. This is not as good as our clear scene test using uniformity constraints among adjacent scenes, but it is extremely good for channels that peak in the upper-atmosphere such as these. The code for this test is extremely simple, and we find the same results, i.e. FOV5 still had the same excess noise.

To determine how much independent gaussian noise must be added to the mean model noise for FOV other then FOV5, we computed what we call \(nedn(5)_{\text{extra}}\) as shown in Eq. 2. This is plotted in Fig. 10 along with the FOV5 ICT noise. This shows that this "extra noise" in FOV5 is almost as large as the ICT noise level. At present we have no explanation for this, other than the observation that FOV5 is more on-axis than the other FOVs and might be susceptible to accidental fringing due to reflections off optical components and their surfaces. Possibly these could be more sensitive to small vibration and mirror movement errors than the radiance interferograms, but this is highly speculative.

\begin{equation} nedn(5)_{\text{extra}} = \sqrt{( nedn(5)_{\text{model}}^2 - \overline{nedn_{\text{model}}^2)}} \end{equation}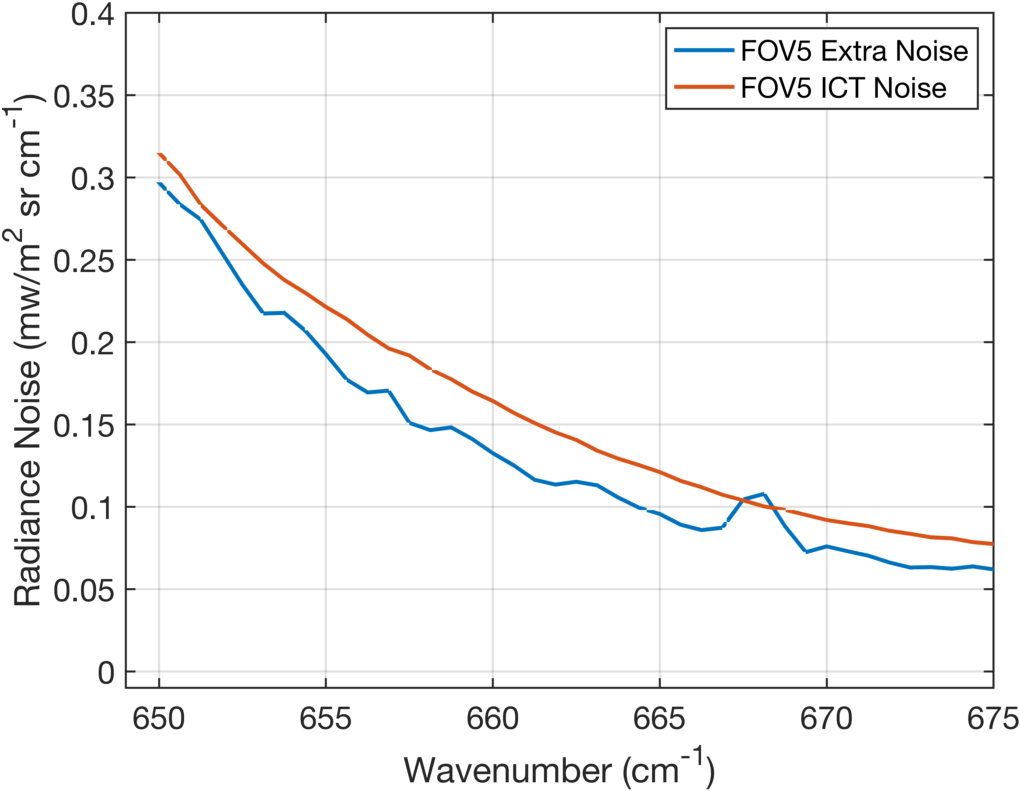

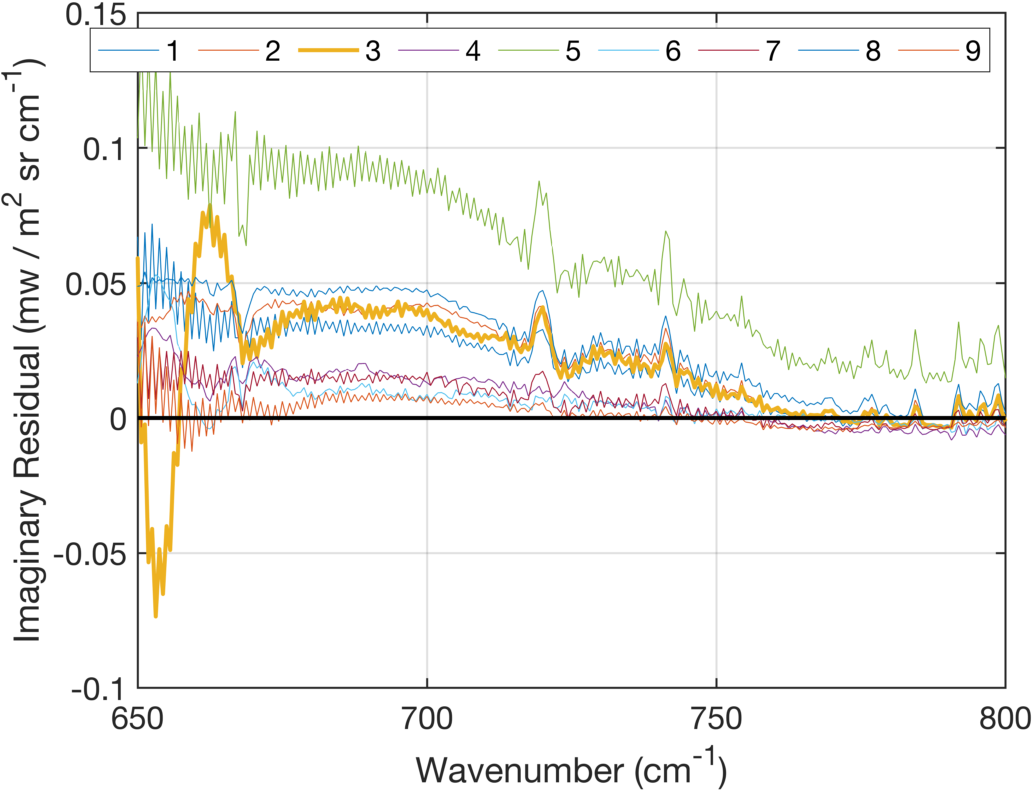
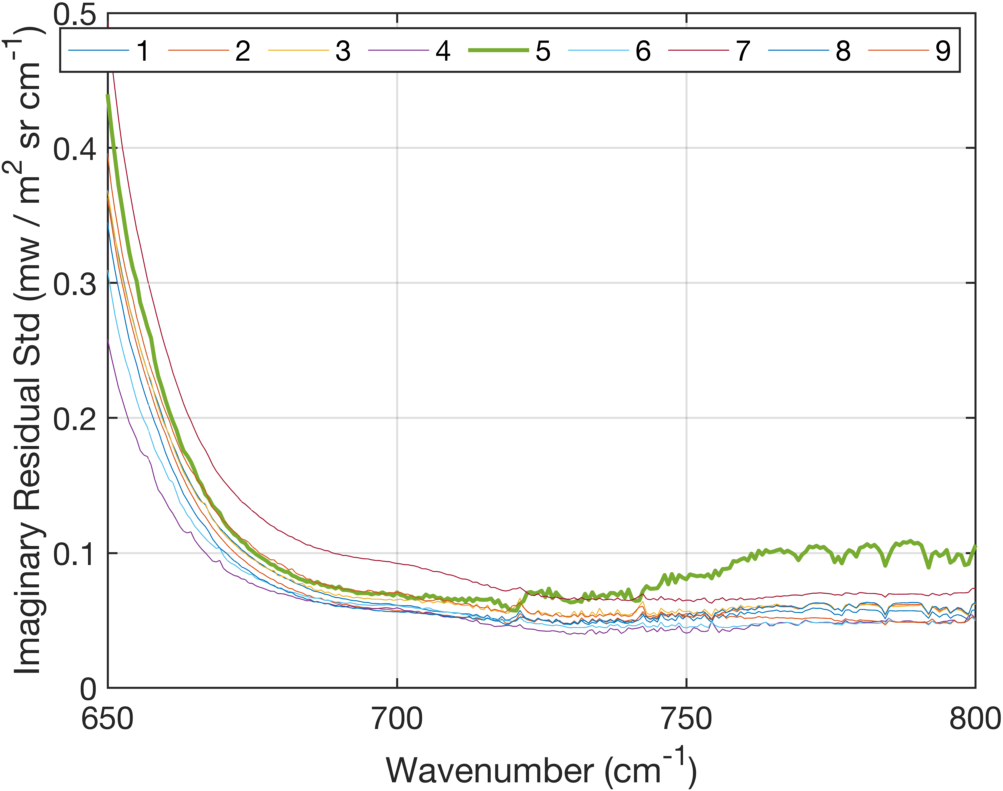
We also examined the complex components of these clear scene radiances. The mean complex residual is shown in Fig. 11 and their standard deviations in Fig. 12. Fig. 11 clearly shows that FOV5 has larger complex components than the other FOVs, all of which are positive except for FOV3. FOV3 exhibits higher variability with wavenumber than the other FOVs. Note that the discussion above suggests that FOV3 seems to have lower noise than it should in the extreme longwave. The complex residual of FOV3 hints that its behavior in indeed out-of-family compared to the other FOVs. The standard deviations of the complex residuals shown in Fig. 12 largely smooth, indicating that the complex radiance residuals are relatively static over time. Note that FOV5 standard deviation does increase above the others past ~750 cm^-1.

As shown in Fig. 4 a number of channels in the shortwave region have bias standard deviations that are close to the instrument noise values, so those regions can be used to understand any anomalous noise characteristics of CrIS FOVs.

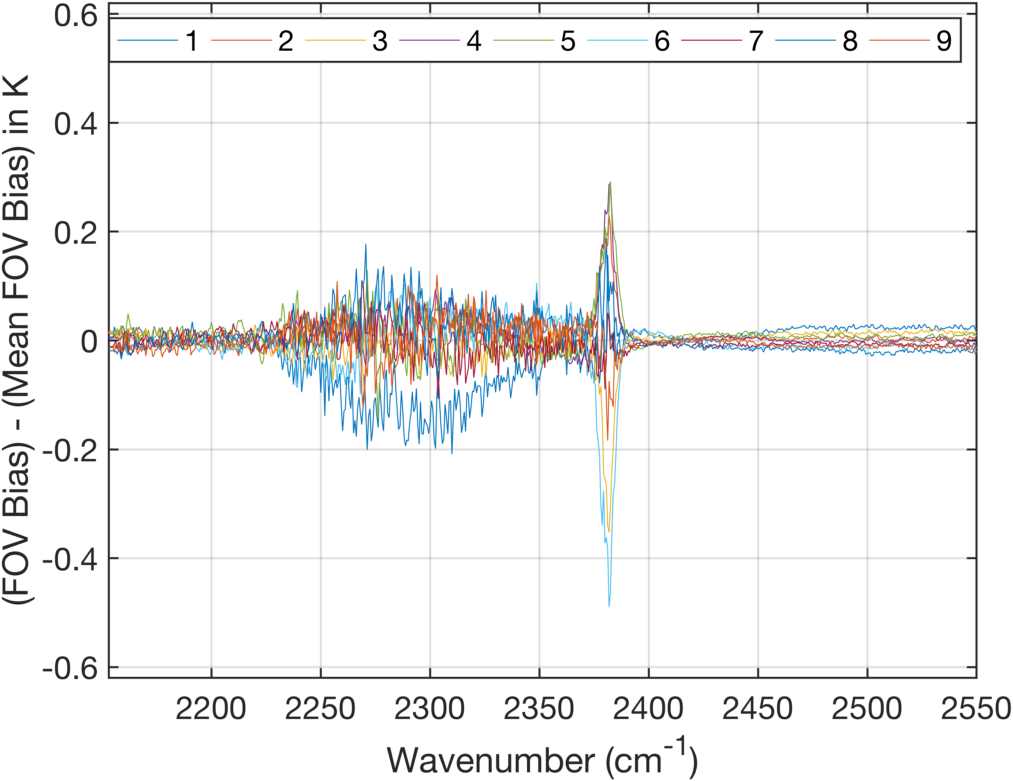
Figure 13 shows the shortwave bias relative to the mean bias (averaged over FOVs). The FOV bias differences are extremely small in the shortwave, the slight offset of FOV1 in the 2250-2350 cm^-1 region is unimportant and far below the noise in this region of very cold BT observations. However, the FOV differences past ~2383 cm^-1 might be important for retrievals (and NWP one day) since these are very good upper-tropospheric sounding channels, and differences of up to ± 0.3K might be important.

The cause of these FOV bias differences in this region are as yet unclear. It does not appear to be a differential frequency calibration error, since that would be largest near 2390 cm^-1 where the slope in the radiance with wavenumber is greatest. A more likely candidate are small errors in either the implementation, or theoretical basis, of the S_a^-1 matrix that removes the effects of self-apodization. Note that 2381 cm^-1 is the region of minimum radiance, which grows by a factor of 3x at 2386 cm^-1.

Parametric studies that vary the FOV off-axis locations should be able to determine if these FOV bias differences are due to an in-accurate focal plane geometry. Note that this spectral region is not used to determine the focal plane geometry since it is quite sensitive to RTA errors. This is less of an issue if we are only looking at relative FOV errors.

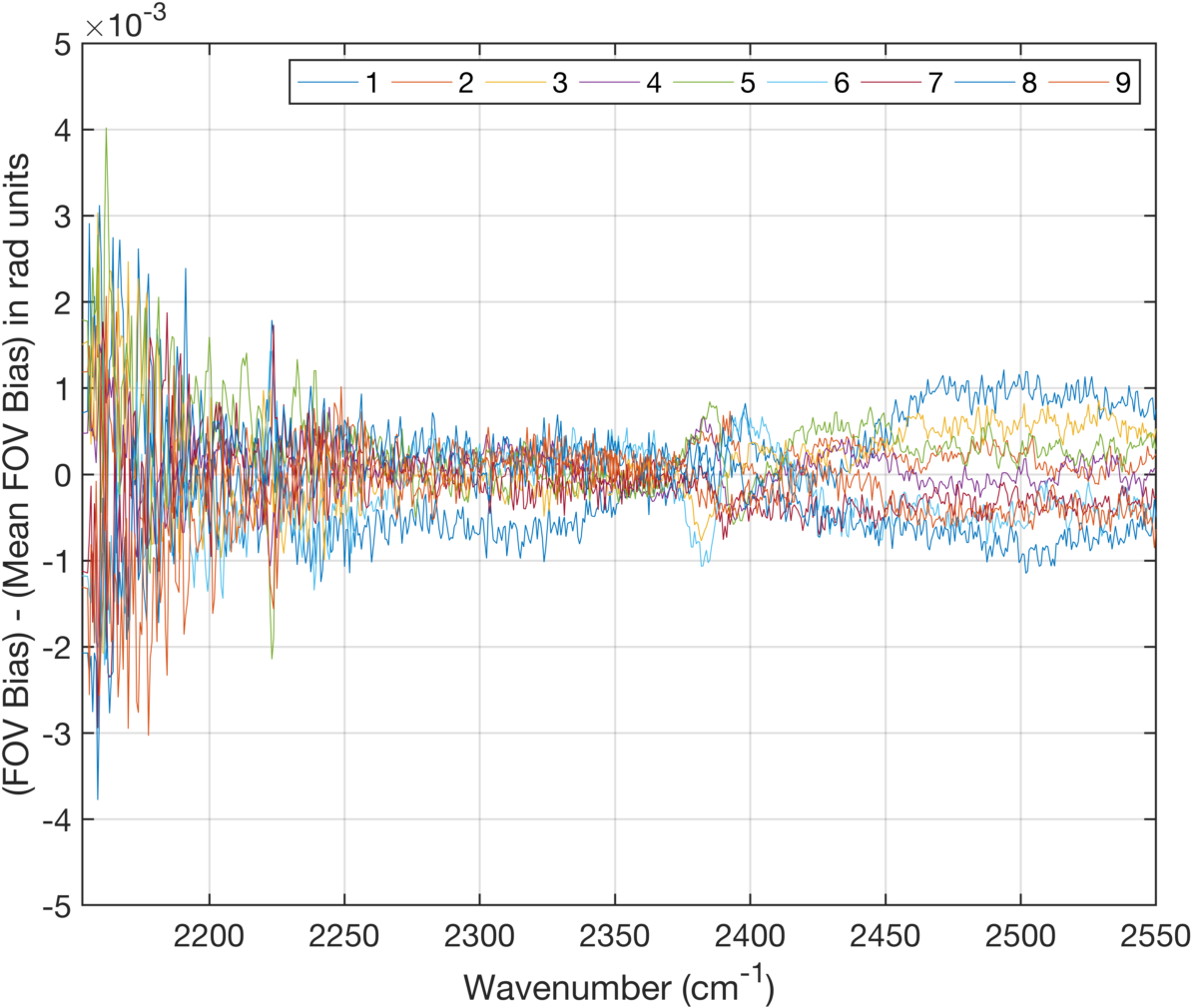
Figure 14 shows the same biases as in Fig. 13 but now in radiance units. This shows that the FOV differences around 2380 cm^-1 are not substantially different than in other regions, but they are magnified when converted to BT by the very cold radiances present in this spectral region.

Figure 15 is a zoom of Fig. 4 in the shortwave, where one can easily see that for some FOVs the shortwave noise is higher than the bias standard deviation. This is unexpected, the bias standard deviations should always be larger than the noise. However, we are using noise generated from the ICT scans that are for a nominal 280K radiance. Since the shortwave noise is dominated by photon shot noise, the scene noise could be different from the ICT derived noise. The results shown in this figure suggest that the ICT noise results are too high for application to the earth scenes. Although there are a number of contributors to the detector shot noise, the scene flux is probably dominant. The integral of the ICT radiance is about 28% larger than the integral of the scene radiance (for these clear tropical ocean scenes), so if photon shot is indeed dominant, once might expect the earth scene noise to be lower than the ICT noise, which is what we appear to be observing.

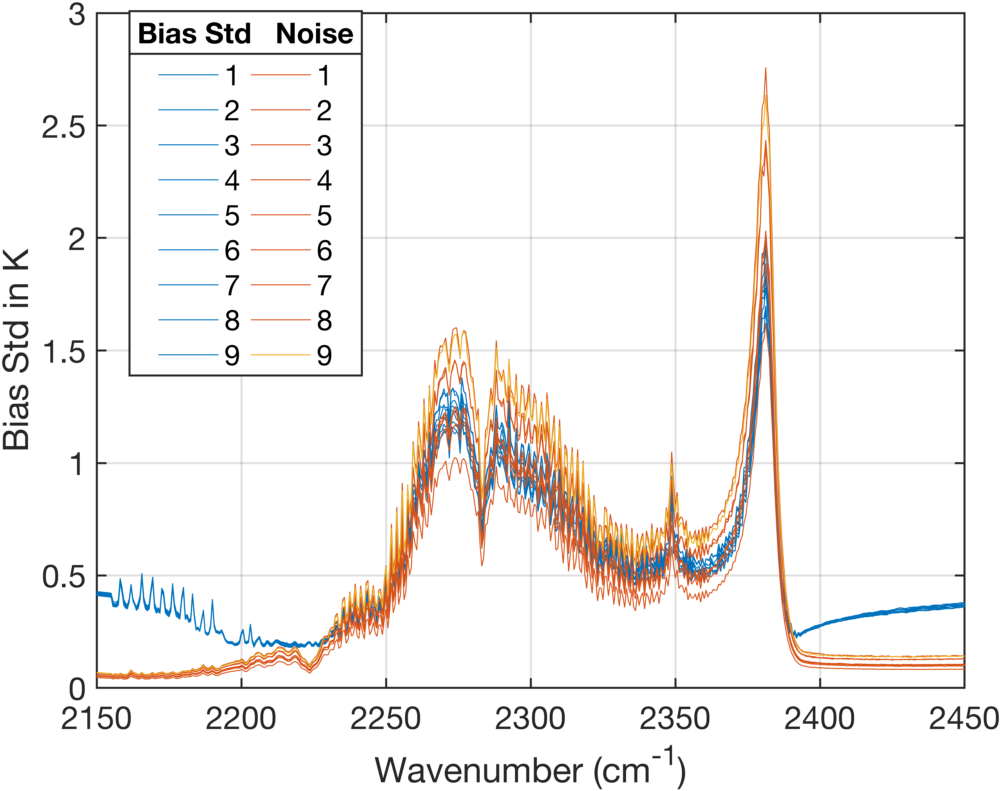
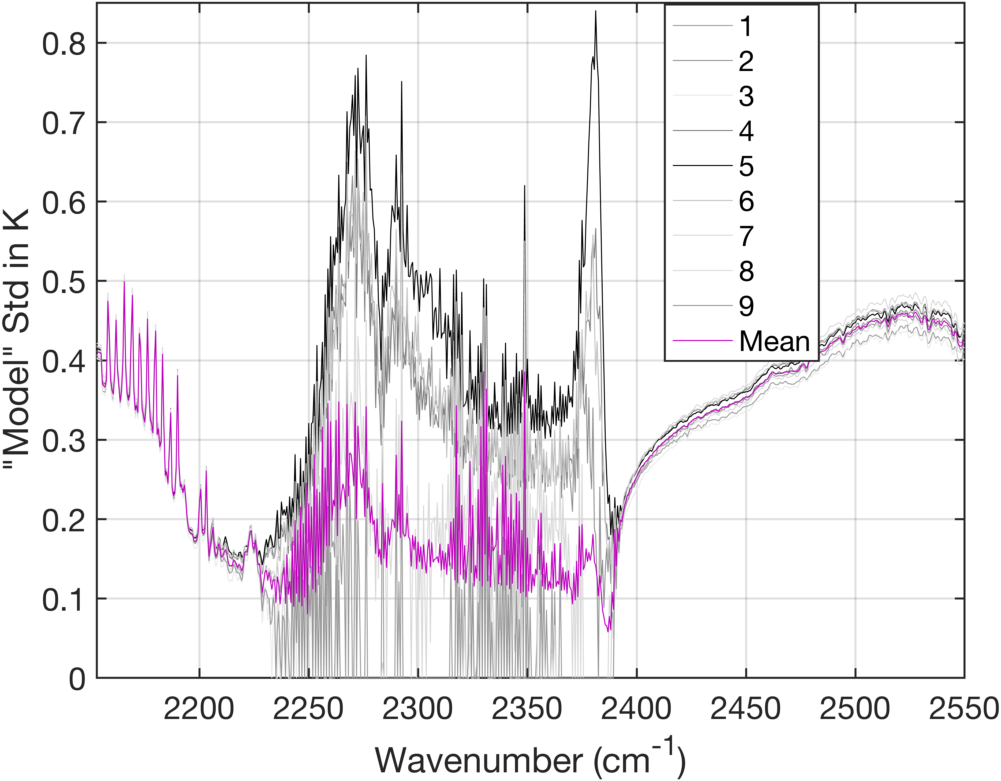
However, this does not preclude us examining the noise characteristics of the different FOVs since the photon shot noise differences from the ICT to the scene should be the same for all FOVs. We now compute the "model noise" for the shortwave spectral region using the same procedures as above. Since the bias standard deviation is sometimes smaller than the shortwave noise figures, this will lead to complex quantities for model noise for some FOVs. To minimize this problem we reduced the ICT-derived noise by 20% for each FOV before applying Eq. 1. Figure 16 is the computed "model noise" in the shortwave, using these modified ICT noise figures.

The mean in Fig. 16 includes all FOVs but FOV3, which produced a complex model noise even with a 20% reduction in ICT noise. This result does show some similarity to the longwave region in that FOV5 is a bit of an outlier and has the largest "model noise".

We note that the midwave has a similar behavior (in the 1620 to 1740 cm^-1 region) where FOV5 also has slightly higher "model noise" than the other FOVs except for FOV9, which has noise so close to the bias standard deviation that the model noise is difficult to compute accurately.

The origin of these differences is not yet clear, or their impact on the scientific use of CrIS radiances. However, we do believe that further work is indeed needed to quantify the exact scene noise in the shortwave especially as that may impact assimilation and retrievals of the very good shortwave upper-tropospheric sounding channels.