AIRS is a grating spectrometer with channel center frequencies that obey the standard grating equation,

\begin{equation} \label{org7853e0b} \nu_{oi} = m/(d * (\sin(\alpha_{1,2}) + \sin(\beta_i))) \end{equation}

where \(m\) is the grating order, \(\nu_{oi}\) the center wavenumber of channel \(i\), d = 77.560 μm is the groove spacing, α the angle of incidence and \(\beta\) the angle of diffraction. AIRS has two incident angles, which we denote \(\alpha_1\) (= 0.55278) and \(\alpha_2\) (= 0.56423). The diffraction angle can be expressed in terms of position on the focal plane using

\begin{equation} \label{eq:2} \beta^k_i = \tan^{-1} \left( \frac{y^k_i}{F} \right) \end{equation}

where \(y_i\) is the detector position in the focal plan, \(F\) is the focal length of the focusing mirror, and \(k\) is an index assigned to each detector module. We use the fact that each AIRS detector is 50 μm wide to write \(y^k_i\) for each array \(k\) as

\begin{equation} y^k_i = y^k_{o} + i*50. \end{equation}

\(y^k_o\) is the position in the dispersed direction of the short wavelength side of each array. Note that the grating order \(m\) can vary with \(k\), as does \(\alpha\). Pre-flight testing of AIRS indicated that a very small correction was needed to model the measured channel centroid frequencies given by

\begin{equation} \label{orged61a9f} \nu_i = \nu_{oi} + a_k \times (\nu_{oi} - \nu_k)^2 \end{equation}

where \(\nu^k\) is fixed for each array to be the nominal center wavenumber of the array, and the parameters \(a_k\) are experimentally determined strow_tvac. These corrections are extremely small, at most 2% of the spectral response function (SRF) width, equivalent approximately 15 ppm fractional change in the centroid frequency. In this document we will often refer to y^k_o as the module Y-offset. The values of \(y_o^k\) were measured during pre-flight testing, and vary from -1.8 to 1.0 cm.

The channel centroid frequencies can drift if either the angles of incidence or diffraction vary. gaiser found that the early in-orbit AIRS frequencies were offset from pre-flight testing value by the equivalent of a Y-offset shift of approximately -13 μm, likely due to launch vibrations. Subsequent examination of the first 29 months of AIRS radiances revealed time-dependent shifts of the AIRS frequencies strow_rta. One purpose of the AIRS L1c product is to remove these trends and provide an AIRS Level 1 product with a fixed frequency grid. In this section we review the methodology used to detect AIRS frequency trends and how they are parameterized for removal from the L1b radiances.

The in-orbit AIRS frequencies are measured on a per module basis by determining the optimum values of \(y_o^k\). The detector spacing is set at 50 μm during the manufacturing of the arrays. Consequently the channel center frequencies are determined by the values of \(y_o^k\) for each of the 17 detector modules. Although the angle of incidence could also change, subsume any incident angle drifts into the diffracted angle drifts, via the observed \(y_o^k\) values.

The module names and their nominal start and end wavenumbers are listed in Table 1. Under ideal circumstances empirical measurements over time of the \(y_o^k\) values for each module would allow computation of the AIRS channel center frequencies via Eq. 1.

Table 1: The wavenumber ranges covered by each of the 17 AIRS detector modules.

Module Name	Start \(\nu\) (cm\(^{-1})\)	End \(\nu\) (cm\(^{-1})\)
m1a	2552	2677
m2a	2432	2555
m1b	2309	2434
m2b	2169	2312
m4a	1540	1614
m4b	1460	1527
m3	1337	1443
m4c	1283	1339
m4d	1216	1273
m5	1055	1136
m6	973	1046
m7	910	974
m8	851	904
m9	788	852
m10	727	782
m11	687	729
m12	649	682

Following strow_rta the module averaged frequency shifts are measured by cross-correlating simulated spectra with the observed AIRS spectra for each module. The simulated spectra were computed using atmospheric model fields from either the ECMWF three-hour forecast/analysis or from the ERA-Interim re-analysis fields. The simulated BT spectra are shifted by the equivalent of Y-offset = 0.01 μm until a peak in the cross-correlation between the observed and simulated spectra is detected. The frequency of the simulated spectrum that gives the maximum correlation defines the optimum Y-offset for the module.

In practice high-quality measurements are not possible for several modules since they contain unsufficient spectral contrast. However, in these cases high-accuracy spectral drift measurements are not required since the spectral contrast is small. Spectral calibration is especially difficult in the m1b modules where there is little contrast, but there is a sharp radiance shoulder from 2380 to 2400 cm^-1 that can confuse the cross-correlation measurement.

Two types of data sets were used to determine and validate the measured frequency shifts.

• AIRS Level-2 cloud-cleared radiances from mission start (Sept. 2002) through mid-2009 averaged every 2 degrees in latitude in 16-day bins.
• AIRS Level 1c (without frequency calibration) clear-ocean scenes separated into 40 zonally-averaged equal-area latitude bin also time-averaged over 16-days.

Simulated radiances were computed with AIRS radiative transfer model (SARTA ccccite:strow_rtax) using the ECMWF/ERA model fields as input. The model fields were co-located with the AIRS observations for each individual spectral radiance. Then the simulated radiances were binned identically to the observed radiances.

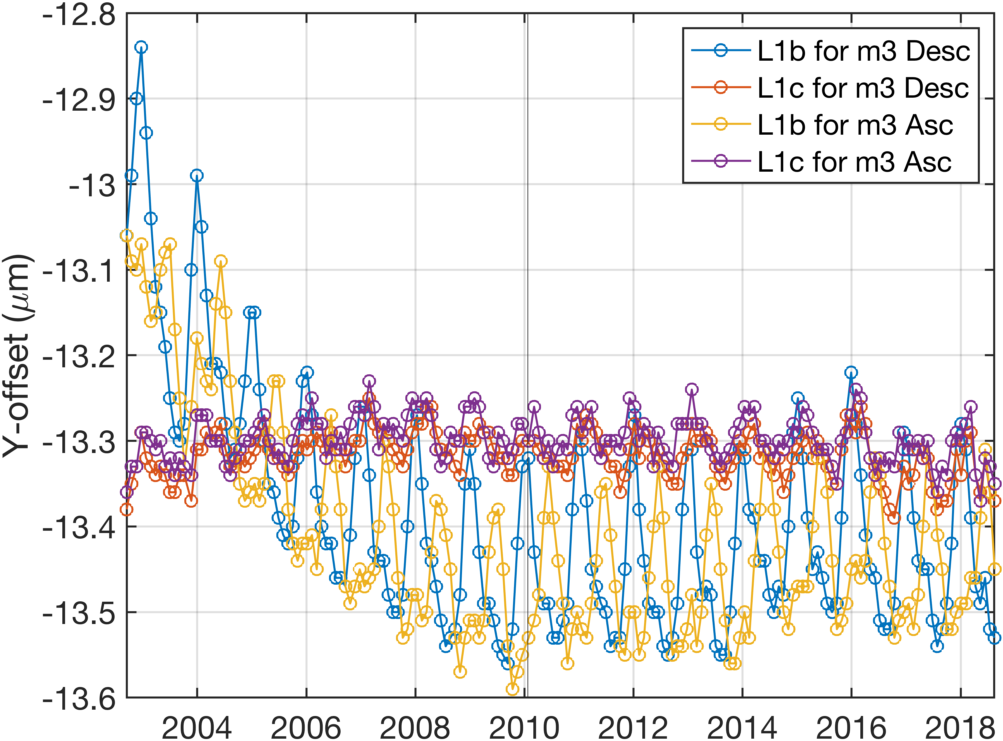
The AIRS Level-2 cloud-cleared radiances were used measure the Y-offsets through mid-2009. Measurements were made every 2 degrees in latitude for both descending and ascending orbits in 16-day increments. The observed AIRS frequency drifts from these data exhibit four types of time-dependent behaviors: (1) A slow secular drift that largely stopped in ~2009, (2) A seasonal variation that appears correlated with the AQUA spacecraft solar beta angle, (3) Periodic drifts that follow the orbit phase, and (4) Sharp jumps that correlate with spacecraft and/or AIRS events such as the Nov. 2003 shutdown of the AQUA platform.

For any given 16-day average, the Y-offsets versus orbit phase for all modules had nearly identical periodic variations with an amplitude of roughly 0.3 μm.

Examination of the derived Y-offsets for each module indicated very similar orbit-phase and longer-term time variations for all modules except m4a and m4c. We found that the m3 module which covers a range of strong water-vapor absorption gave the most stable set of Y-offset measurement, especially as a function of orbit phase. For example, the peak cross-correlation of this module with simulated spectra was quite high, but more importantly, was nearly constant over all latitudes for both ascending an descending orbits. Consequently, we used the m3 Y-offset data to parameterize the orbit-phase and longer-term time dependence of the AIRS detectors. As discussed below, the long-term time dependence of the m4a and m4c modules was slightly different, so they were parameterized separately.

A per-module mean Y-offset was determined using the 2002 to 2009 data. These offsets were quite small, varying by ~1 μm and centered roughly between -13 and -14 μm compared to the pre-launch values. Over the full mission we found Y-offsets for all modules to vary at most by -12.4 to -14.3 μm.

The origin of these Y-offset shifts is likely small thermally induced shifts in the detector focal plane positions, or shifts of the spectrometer optics. The secular drift might be related to equilibration of the sensor after launch. AIRS is highly temperature controlled so one would expect any drifts to be small. The seasonal variation has a pattern similar to the AQUA solar beta angle, suggesting slight thermal movements of AIRS depending on the amount of solar heating during the year. This could also be related to the upwelling albedo emission. The periodic orbital drifts are presumably caused by the periodic variation in solar heating during each orbit.

AIRS has had several events during the mission, these include the AQUA shutdown in Nov. 2003, and two AIRS-only events (cooler issues) in January 2010 and March 2015 that apparently induced small offsets in the frequency shifts. These were measured using the m3 module, but were also found in other modules, including m10 and m12. These offsets are included in the parameterization of the Y-offsets versus time.

Figure 1 shows the time-dependence of the Y-offsets for most modules up to mid-2009. The mean Y-offsets for each module have been removed to illustrate how similar the modules vary in time. Modules m4a and m4c are plotted separately since their secular shift varys more slowly in time (more linear then exponential). Although not clearly evident in this plot, the seasonal variations have shoulders that are similar to the AQUA solar beta angle, later plots will show this more clearly.

The 2002 to 2009 date was used to parameterize the shifts of each module versus time and orbit phase as follows. Modules m4a and m4c appear to be changing more linearly in time than the others, and were parameterized as shown below.

\begin{equation} \label{org6e3163c} y_o^k = y^k_{\textrm{pre-flight}} + a_1^k - a_2\Delta t + \sum_{i=1}^2 c_i \sin(2i\pi\Delta t + d_i) \end{equation}

where we set \(y^{k}_{\mathrm pre-flight}\) to -14 μm. The other modules were also parameterized with Eq. \eqref{org6e3163c} for the pre-Nov. 2003 data only. The time span of the pre-Nov. 2003 data was insufficient for detecting/modelling with an exponential, which is used for data after Nov. 2003.

The \(a_1^k\) are the time-independent offsets of each module relative to the pre-flight value. All the \(a_1^k\) have the same relative dependence on orbit phase, so they only differ by a constant. \(a_2\) is the amplitude of the module Y-offset drift where Δ\(t\) is either the time since launch, or the time since the Nov. 2003 AQUA shutdown. Therefore there are two distinct sets of coefficients, mission start to Nov. 2003, Nov. 2003 to the present. The \(\sin\) terms, \(c_{1,2}\), and \(d_{1,2}\), are identical for all arrays and only vary slightly with orbit phase.

For the other modules after Nov. 2003 we switch to greek notation for the parameterization constants, and now use an exponential term for the secular drift:

\begin{equation} \label{org85a06fa} y_o^k = y^k_{\textrm{pre-flight}} + \alpha_1^k - \alpha_2 \exp^{-\Delta t/\alpha_3} + \sum_{i=1}^3 \beta_i \sin(2i\pi\Delta t + \gamma_i) \end{equation}

As in Eq. \eqref{org6e3163c} the \(\alpha_1^k\) parameters are time-independent offsets of each module but with identical dependence on orbit phase. The \(\alpha_2\) parameters vary slightly with orbit phase but are identical for all arrays (except m4a and m4c which use Eq. \eqref{org6e3163c}). The decay rate of the exponential, \(\alpha_3\), is the same for all orbit phases and modules. The orbit phase dependence of the higher order terms (β_1-3 and γ_1-3) are identical for all modules, and again vary only slightly with orbit phase. The orbit phase dependence of the \(\sin\) terms are identical for all arrays and mostly only modify the ascending part of the orbit (when solar radiation is hitting the spacecraft).

In summary, with regard to orbit phase dependence, all terms except the \(a_2\) and \(\alpha_2\) parameters depend on orbit phase, identically for all modules. However, all but about 20% of the orbit phase dependence are provided by the \(a_1^k\) and \(\alpha_1^k\) parameters.

Figure 3 shows an example of the time dependence of \(y_o^{m3}\) near the equator for both descending and ascending passes. Most evident is the steep secular negative increase in early years that levels out in the 2009 time range. Also evident are the seasonal cycles and the inversion of the amplitudes between ascending and descending. There are small "shoulders" on the nearly sinusoidal oscillation in the April-June time that one sees in a plot of the AQUA solar beta angle, suggesting that solar heating of the spacecraft is dominating the seasonal variability. Although difficult to see in this plot, small shifts due to AIRS shutdowns occur in Nov. 2003, Jan. 2010, and March 2014.

Given an accurate model for the frequency shifts of each channel in AIRS, we can then interpolate the measured spectra with a time-varying frequency grid to a fixed frequency grid. This is an essential step for accurate studies of radiance trends, and allows the use of a single frequency grid radiative transfer model for AIRS retrievals.

The frequency shifts required to put the AIRS radiances on a fixed grid are quite small, with maximum shifts of ~10 ppm in frequency. (The influence on brightness temperatures will be introduced later.) A 10 ppm shift corresponds to moving a channel radiance by about 2.5% of the channel spacing. This could be done by interpolating the radiances on the observed frequency scale (from the above discussed model) to a fixed frequency scale using a cubic spline. However, this is relatively error prone due to the large spacing of the AIRS channels relative to the small interpolations needed. The spline interpolation to the fixed frequency grid is improved by modifying the spline derivative using small regression coefficients as follows,

\begin{equation} \label{org6e98c7a} BT_{l1c} = BT_{obs} + \left[a \left(\frac{\partial BT}{\partial \nu}\right)+b\right]\delta \nu. \end{equation}

where \(a\) and \(b\) are linear regression coefficients, for each channel, that are derived from simulations. \(BT_{l1c}\) is the correct brightness temperature for the fixed frequency Level 1c grid, \(BT_{obs}\) is the observed brightness temperature, and \(\delta\nu\) is the frequency difference between the observed and fixed grids. The \(BT\) derivative is computed from

\begin{equation} \frac{\partial BT}{\partial \nu} \equiv \frac{BT_{obs} - BT_s}{\delta \nu} \end{equation}

where \(BT_s\) is a spline fit to \(BT_{obs}\) evaluated at the \(\nu_{l1c}\) freqencies.

Simulated data were created using the kCARTA pseudo line-by-line radiative transfer algorithm kcarta for 49 highly variable profiles that largely span global profile variability. (These profiles are used to create the AIRS SARTA forward model strow_sarta). The monochromatic simulations are convolved with the AIRS spectral response functions for -13 and -14 μm frequency offsets. Then Eq. \eqref{org6e98c7a} is used with the simulated data to regress for \(a\) and \(b\) for each channel.

These regression coefficients reduce the application of Eq. \eqref{org6e98c7a} with simulated data from errors of up to 0.05K in \(BT\) to errors well below 0.01K. The channel average of \(a\) coefficients are close to unity with a standard deviation of 0.6. The channel average of the \(b\) coefficients is near zero with a standard deviation of 0.9. Note that \(b\) coeffients are multiplied by the frequency offset between the observed and fixed frequency grid, generally very small numbers in the in the range of 0.005 to 0.025 cm^-1. On average the \(a\) and \(b\) coefficients modify the BT interpolation by ~14% and ~7% respectively.coefficients Given that the AIRS detector noise values are nominally around 0.2K, the frequency shift corrections are only seen in averaged data, especially as a function of time.

The fixed frequency grid for the AIRS L1c product was chosen to be our measurement of the AIRS observed frequency grid on January 20, 2010 at the first descending equator crossing. This is a somewhat arbitrary choice. Factors for this choice include: (1) By this date the secular shift of AIRS had pretty much stopped, and (2) Just before this date AIRS had a shutdown which caused a small 0.04 μm Y-offset shift, and thus we avoid interpolations for this shift after that date.

The accuracy of interpolation of AIRS observed radiances to the L1c fixed frequency grid were tested over the full mission (to date) for seven of the AIRS modules (m3, m4a-d, m10, and m12). Figure 4 shows the variation in Y-offsets versus time for range of ascending and descending latitudes (orbit phases). These curves illustrate the orbit phase dependence of the frequencies as well as the overall seasonal variations and secular trends. A positive shift in the Y-offsets is somewhat evident in these curves after 2014, which is due to the AIRS March 2014 shutdown. The right-hand-side of this figures are the retrievals of the Y-offsets from L1c radiances after interpolation to a fixed frequency grid. Most of the time and orbit phase dependence of the frequencies is now gone and the residual variations are less than ±0.1 μm

Similarly we show the same multi orbit phase data for the m10 array in Fig. [[m10all]. The seasonal and secular trends are almost completed removed. A small error in the orbit phase dependence seems evident but is small enough to be ignored.

Figure 6 shows the m3 module time series of Y-offsets derived from the original un-corrected L1c data and after the radiances are shifted to the L1c fixed frequency scale. We show both ascending an descending nodes for a latitude of -1.4 ± 2.8 degrees. The vertical black line at January 22, 2010 indicates the time chosen for the fixed frequency scale, where it correctly matches the descending node value before correction.

As noted above, the Y-offset time and orbit-phase dependence is identical for all modules except for m4a and m4c. We illustrate in Fig. 7 an example of why this simplification is justified, where we plot both the m3 and m10 calibrated Y-offsets before introducing the 0.056 μm offset that took place in March 2014. The m10 Y-offset is first plotted without any adjustment, showing the displacement in Y-offset units between these two arrays. (Note the m10 array uses CO₂ lines for the frequency retrievals, while m3 uses H₂O lines.) One can clearly see that the Y-offset shift in Marchc 2014 is essentially identical in both arrays. If we overlay the m10 curve with the m3 curve by adding a 0.21 μm offset for plotting purposes, this agreement is extremely clear. Moreover, it appears that much of the remaining short term variations are quite similar in both arrays, as might be expected.

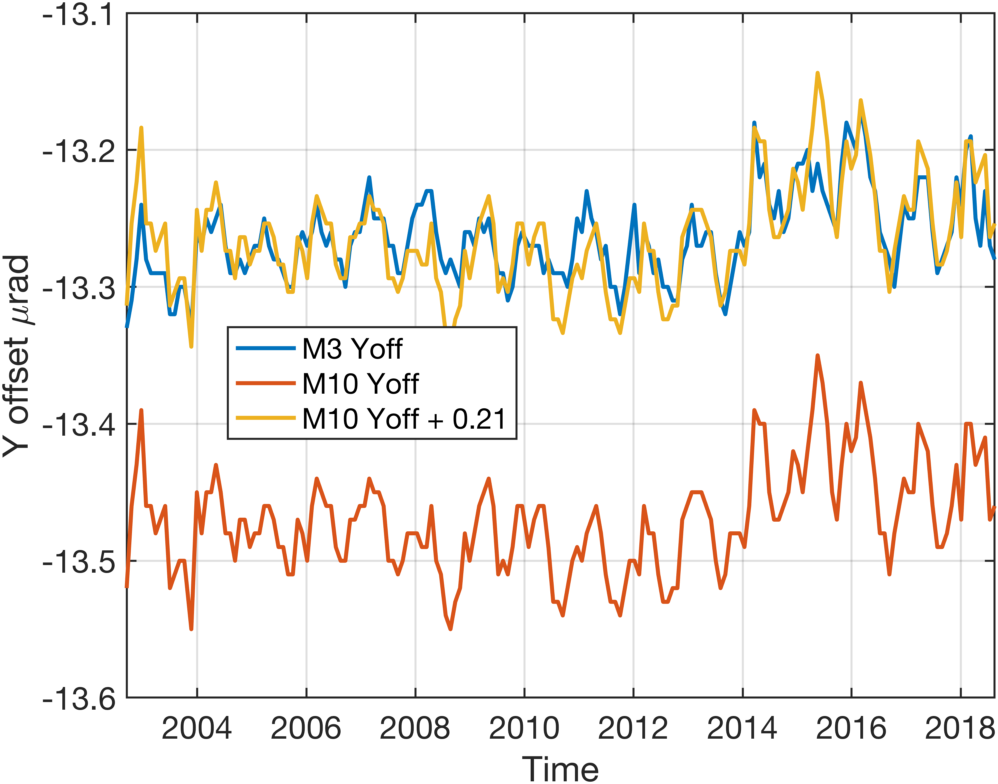
Figure 8 shows the un-calibrated L1b and calibrated L1c frequency shifts for all of the m4 modules. The m4b and m4d modules (right hand side of Fig. 8) use the same Y-offset model as the other non-m4 modules. Although the frequency calibration of these two modules greatly improves the frequency stability, it is clear that a small drift down in Y-offset is present, with a total drift of about 0.2 μm over 17 years. This is small enough to be ignored for most applications, but we will re-visit this issue in future updates to the L1c frequency calibration.

As noted earlier, m4a and m4c (left hand side of Fig. 8) frequency drifts are treated differently than the other AIRS modules by using a linear versus exponential term for the secular drift. This appears to continue to be a good model for m4a, m4c. However, there is a striking offset in these two modules that starts directly after the March 2014 AIRS shutdown. Apparently this shift recovers after about two years. At this time, we have not implemented any fix for these frequency shifts. There is the possibility that these apparent frequency shifts are not true frequency shifts but radiometric offsets that corrupt the cross-correlation frequency shift measurement algorithm. More work is needed to fully understand this issue and correct any offsets.

The m4a and m4c modules may behave differently than the others because the module mounting material is different for m4a and m4c (versus m4b and m4d) which could a differential response in the module positions due to thermal disturbances.

The impact of the L1c frequency scale corrections on brightness temperatures is small, but important at the climate level. First, it is important to understand that most of the L1b errors due to a shifting frequency scale are only easily measured on the sides of AIRS absorption/emission lines. Most retrieval algorithms that are trying to limit the number of of channels used in a retrieval, or data assimilation, avoid using this class of channels since their weighting functions are often either complicated or quite broad. However, for climate trend studies the highest level of stability is needed.

Figure 9 shows the maximum differences seen in the AIRS brightness temperature over the first 17 years of the mission in blue, for a clear-ocean tropical scene. These are mostly dominated by the secular drifts in frequency from 2002 through 2007. As shown here there are also seasonal frequency shifts and shifts during every orbit. The maximum orbital variations (which are always present) are shown in red, and our estimated maximum uncertainties in the AIRS brightness temperatures in the L1c product due to interpolation to a fixed frequency grid. This last curve is plotted separately in Fig. 10 showing that the maximum brightness temperature uncertainties are ~±0.06K.

A histogram of these L1c uncertainties is shown in Fig. 11 where one immediately sees that the vast majority of channels have errors due to uncertainties in the frequency intepolation below 0.01K (note that that count scale has been truncated at 400, it peaks at 1488 counts).

There are some channels that are likely needed for climate-level studies that are quite sensitive to the AIRS frequency drifts. The 2382 to 2395 \wn channels of AIRS are heavily used in the AIRS Level-2 retrievals since that regions has low detector noise, the channels are almost solely due to CO² emissions, and their Jacobians are highly sensitive to temperature. Without frequency correction, the channels in this region will vary by ~0.13K over the mission, about 10X higher than projected climate warming. The estimated maximum uncertainty in the frequency shifted L1c calibration for these channels is about 0.027K, possibly large enough to affect climate-level trend retrievals.

In the longwave tropospheric CO₂ sounding regioin from 710 to 770 cm^-1 there are many channels inbetween spectral lines that are largely unaffected by frequency shifts. However, there are also many channel in this region that have liens are there radiometric stability due to shifts in A/B detectors during the mission, and due to possible small radiometric drifts in A-alone or B-alone detector channels. Work in progress indicates that without the use of channels on the sides of lines that very few (~10) channels remain that are not affected by frequency shifts, which likely requires use of channels sensitive to frequency shifts for full-profile retrievals. This analysis is far from definitive, it's purpose here is to caution the user that other factors might force use of channels sensitive to frequency shifts.

The AIRS observations are doppler shifted due to the rotation of the earth seen from the AQUA spacecraft. These shifts are largest at the equator for high scan angles, and switch sign as AIRS scans through nadir. The doppler shifts can be computed from (chen)

\begin{equation} \label{orga9cf007} \Delta\nu_{\textrm{doppler}} = \pm\frac{\Omega R_e}{c} \sin(\theta_{zenith}) \cos(lat_{sub}) |sin(\theta_{azimuth})| \end{equation}

where, Ω = 7.292 × 10^-5 (earth's rotational velocity, rad/sec), R_e = 6.3781 × 10⁸ (earth radius, cm), and c = 2.99792 × 10¹⁰ (speed of light, cm/sec). The leading plus sign corresponds to xtrack 1:45 for ascending nodes and xtrack 46:90 for descending nodes, while the minus sign is for xtrack 46:90 for descending nodes and xtrack 1:45 for ascending nodes.

The maximum value of these doppler shifts is about ±1.4 ppm of the channel wavenumber, which varies from 0.91 to 3.7× 10^-3 cm^-1. In units of Y-offset shifts this is about 0.16 μm. (Note that the doppler shifts are true shifts in the AIRS observations, not instrument induced.) Although small, these are easily observable with the same algorithm that was used to measure the AIRS instrument frequency drifts. The main controlling variables are latitude and cross-track position.

Figure 12 shows the measured and computed Doppler shifts as a function of latitude for both ascending and descending orbits. Plotted is the mean doppler shift difference between either side of nadir by subtracting the doppler shift for xtracks 46-90 from those for xtracks 1:45. Note that nadir is halfway between xtracks 45 and 46. These measurements were done using a 32-day average of clear tropical ocean scenes for 20 equal-area latitude bins. Note the correct switch in sign in the Doppler signal for ascending versus descending orbits. The agreement between theory and observed shifts is excellent, especially considering that the maximum signal in this plot is only ~1.4 ppm.

Since the largest effect is at the equator, we examine the xtrack dependence of the doppler signal near the equator (-1.4^o latitude) that is ± 1.4^o wide in Fig. 14. We again see close agreement between the observed and computed doppler shifts. Finally in Fig. 13 we show the same measurements as in Fig. 14 except for a latitude zone centered at -39^o with a width of ± 3.7^o. Agreement is again quite good, although there is some noise at the higher cross-track positions, which is expected since there are both fewer clear scenes detected in the mid-latitude than the tropics and fewer clear scenes at higher scan angles.

The L1c radiances are all interpolated to a fixed frequency scale, \(\nu_{l1c}\), as defined above to be the observed channel frequencies on January 22, 2010 for the first descending node crossing of the equator. The time-dependence of observed AIRS frequencies, \(\nu_i\), are computed from Eqs. \eqref{org7853e0b} and \eqref{orged61a9f} using the \(y_o^k\) values given by either Eqs. \eqref{org6e3163c} or \eqref{org85a06fa}, depending on whether the observations if before or after the November 2003 shutdown. The final Level 1c radiances are derived by interpolating the observed radiances to the \(\nu_{l1c}\) frequency scale taking into account the instrument frequency shift while also removing the doppler shift using Eq. \eqref{org6e98c7a}. This is implemented by using

\begin{equation} \delta\nu = (\nu_i - \nu_{l1c}) - \Delta\nu_{\mathrm{doppler}} \end{equation}

where \(\delta\nu\) was introduced in Eq. \eqref{org6e98c7a}.

The Level 1c product includes 331 channels for which there is no corresponding Level 1b radiance product. These so-called "fill channels" are described in detail above, and provide reasonable estimates of what the observed radiance would be for each Level 1c spectrum if those channels were actually measured. Although significant use of these fill channels for scientific purposes should be avoided, there may be cases where they provide sufficiently accurate information. The purpose of this section is to provide an estimate of the accuracy of these fill channels.

The most straightforward way to estimate the fill channel accuracies are via intercomparisons with IASI, since IASI contains channels in all of the fill channel spectral regions. Simultaneous nadir overpasses (SNOs) between IASI and AIRS occur in the vicinity of either +82 or -82 degrees latitude. One year's worth of AIRS and IASI1 (METOP-1) SNOs were collected. IASI and AIRS have similar spectral response functions in the longwave, while IASI has higher spectral resolution than AIRS in the midwave and shortwave. Here we convert the IASI SNO's to the AIRS spectral response function using an approach similar to that employed by motteler to convert AIRS to the CrIS spectral response functions. This approach is very accurate, especially compared to the radiometric differences between IASI and AIRS, and even more so compared to the fill channel accuracies.

Figure 15 shows the mean of one year's worth of SNO spectra for both instruments, plotted using their native spectral responses. The AIRS L1c fill channels are denoted in this figure with green circles. After conversion of IASI to the AIRS spectral response, we plot the brightness temperature differences between AIRS and IASI in Fig. 16. The colors denote different AIRS modules, and the fill channels are plotted in gray with circles. The statistical uncertainties in this figure are extremely small compared to the observed mean differences.

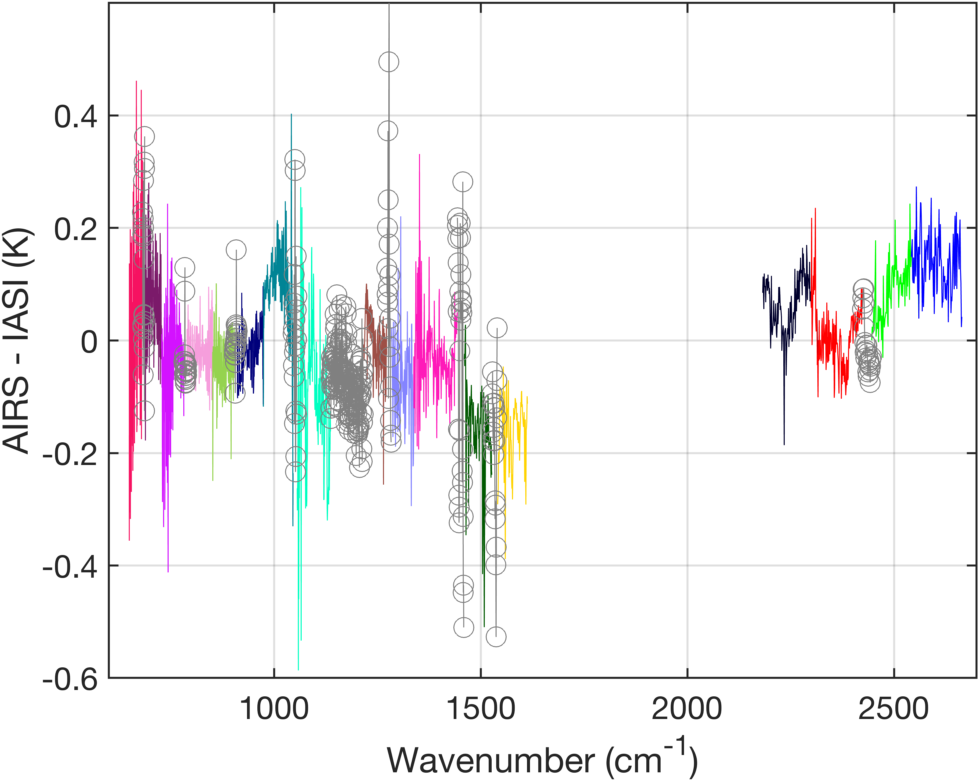
The overall radiometric differences between IASI and AIRS are roughly similar to those between CrIS and AIRS converted to the CrIS spectral response in terms of overall shifts between modules and offsets in modules m4a and m4b relative to m3, m4c, and m4d (see Table 1). In a general sense, the fill channel differences are similar to those for actual Level 1c channels with slightly higher spread. Somewhat higher deviations between AIRS and IASI are seen in the mid-wave water band. Figure 17 is a zoom of Fig. 16 in that region where one can easily see that errors in the fill channels in this region are larger than any differences between AIRS and IASI for measured channels. This figure indicates that the water region fill channels likely have maximum errors less than ±1K. Future improvements in the fill channels should concentrate on the water band gaps.

Figure 18 illustrates the probably of occurance of L1c using a synthetic values for a channels's radiance. These data were collected over ~20 days using a total 5036 channels. Note that changes in a detector operating characteristics at any time during the mission can change the percentage occurances seen in this particular snapshot of AIRS Level 1c.

Bibliography

• [strow_rta] Strow, Hannon, Machado, Motteler & Tobin, Validation of the Atmospheric Infrared Sounder radiative transfer algorithm, Journal of Geophysical Research: Atmospheres (1984–2012), 111(D9), (2006). link. doi.
• [strow_tvac] Strow, Hannon, Weiler, Overoye, Gaiser & Aumann, Prelaunch spectral calibration of the atmospheric infrared sounder (AIRS), IEEE Transactions on Geoscience and Remote Sensing, 41, 274-286 (2003). doi.
• [gaiser] Steven Gaiser, Hartmut Aumann, Larrabee Strow, Scott Hannon & Margaret Weiler, In-flight spectral calibration of the Atmospheric Infrared Sounder, IEEE Trans. Geoscience and Remote Sensing, 41, 287-297 (2003).
• [kcarta] Strow, Motteler, Benson, Hannon & Souza-Machado, Fast computation of monochromatic infrared atmospheric transmittances using compressed look-up tables, Journal of Quantitative Spectroscopy and Radiative Transfer, 59(3-5), 481-493 (1998). link. doi.
• [strow_sarta] Strow, Hannon, Souza-Machado, Motteler & Tobin, An overview of the AIRS radiative transfer model, IEEE Transactions on Geoscience and Remote Sensing, 41, 303-313 (2003). doi.
• [chen] Yong Chen, Yong Han & Fuzhong Weng, Detection of Earth-rotation Doppler shift from Suomi National Polar-Orbiting Partnership Cross-Track Infrared Sounder, Appl. Opt., 52(25), 6250-6257 (2013). link. doi.
• [motteler] Motteler & Strow, AIRS Deconvolution and the Translation of AIRS-to-CrIS Radiances With Applications for the IR Climate Record, IEEE Transactions on Geoscience and Remote Sensing, 57, 1793-1803 (2018). doi.